Goed. Als ik het goed begrijp, wil je een volgende setup maken:
Bekijk bijlage 1915
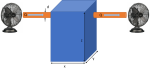
De blauwe box is de koelkast en de oranje pijp de koperen buis. Waarin d de diameter van de buis, Q de lucht flow en x, y, z de afmetingen van de koelkast. Ik ga overal uit van de binnen afmetingen van de koelkast, dus het is echt de ruimte die je gekoeld hebt, en niet de ruimte die je koelkast inneemt in je garage. In de koelkast wil je de buis zoveel mogelijk lengte laten afleggen, dus ziet het er ongeveer zo uit:
Bekijk bijlage 1916
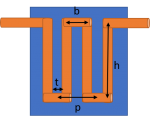
Met p de afstand van 1 kronkel en h grofweg de hoogte van de koelkast. De hoeveelheid kronkels die je kunt maken hangt af van de dikte van de pijp (d), de lengte van de tussenstukjes (t) en de breedte van de koelkast zelf (x). Als we zeggen dan t = d (dan maak je een aardig strakke bocht), dan komen we erop uit dat het aantal kronkels

is als volgt:
n = x / 4d
(Note dat b = 2*d, dus p = 4*d.)
((Note ook dat het aantal kronkels altijd een rond getal moet zijn. Je maakt geen 7.7 kronkels zeg maar))
De totale lengte (Ltot) die je hebt is dan de lengte van 1 kronkel * het aantal kronkels.
Ltot = (x/4d)*(2*h+4*d)
De hoogte h kunnen we hetzelfde nemen als de hoogte van de koelkast, dus h=z. Het volume van de buizen in de koelkast is gelijk aan de lengte * het oppervlak. Dus:
Vtot = pi*(d/2)^2*Ltot
Je kunt je voorstellen dat het volume van de buizen groter wordt met een grotere diameter, maar daardoor kun je ook minder kronkels maken.
Laten we nu de diepte van de koelkast in acht nemen. Ook hier weer, hoe dikker de buis, hoe minder kronkels je naast elkaar kan zetten. Het aantal "rijen van kronkels" naast elkaar is berekend op een vergelijkbare manier: m = y / 4d
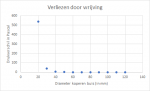
Omdat m en n een exact getal moeten zijn (en naar beneden afgerond moeten worden), ga ik dit probleem niet analytisch maar numeriek uitrekenen. Het gevolg is de volgende plot.
Bekijk bijlage 1917
De grafiek verspringt heel systematisch, maar ook dat heeft te maken met het feit dat n en m afgeronde, hele getallen zijn. Als de buis te groot wordt (>110 mm), kun je niet eens 1 kronkel maken, dus dan heb je effectief geen volume in de koelkast. Ik heb arbitraire dingen ingevuld voor de afmetingen van de koelkast, dus deze grafiek is slechts een indicatie.
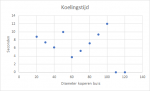
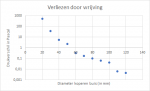
Dit is alleen niet het enige interessante. We willen ook weten hoelang de lucht in de koelkast verblijft. De lucht gaat natuurlijk sneller door een smalle buis, maar een smalle buis is veel langer. De snelheid van de lucht is uit te rekenen door de totale flow door de oppervlakte van de buis te delen. (v = Q/A). Ik heb opgezocht dat een gemiddelde ventilator 100 kubieke meter lucht per minuut beweegt. De verblijftijd van de lucht in de koelkast is als volgt is berekend door de snelheid van de lucht:
Bekijk bijlage 1918
Uiteraard heeft deze grafiek veel gelijkenissen met de vorige: Zowel het volume van de buizen als het aantal seconden dat de lucht in de koelkast is, is heel erg afhankelijk van de buis lengte in de koelkast.
-- In principe kunnen we al stoppen. Want in 12 seconden wordt lucht bij lange na niet koud genoeg om te kunnen koelen. Maar goed, we gaan door --
De verliezen door wrijving zijn ook interessant om te zien. Door alle wrijving ontstaat er warmte, en dat is precies niet wat we willen hebben. Dus we zoeken het scenario met de minste wrijving. Wrijving bij stromingsleer bestaat uit 2 delen: Major losses en Minor losses. De major losses zijn de verliezen doordat de lucht langs de wand van de buizen schuurt, en de Minor losses zijn de verliezen die ontstaan door extra wrijving door een specifiek onderdeel (zoals een bocht). Hoe meer kronkels, hoe meer bochten en buislengte. Dus, hoe meer wrijving. Ook de aansluiting van de ventilator op het systeem moet meegenomen worden (dat is ook een onderdeel). De verliezen bereken ik als drukverschil. Dat wil zeggen, doordat de lucht door een systeem heen gaat, verliest het interne energie (druk) en wordt dat warmte. Dus hoe minder drukverschil, hoe beter. Als ik koper als materiaal gebruik, kom is op de volgende:
Bekijk bijlage 1919
En dan ff op logaritmische schaal:
Bekijk bijlage 1920
Dus we zien dat het eerste scenario helemaal niet handig is.
Ik heb de koelkastmaten als 40x40x60 cm genomen. Als we even de verblijftijd in de koelkast negeren, zou ik de 50 mm diameter buis aanraden. Maar een andere koelkast heeft wellicht compleet andere resultaten, omdat je precies dan extra kronkels naast elkaar kan leggen bijvoorbeeld.
En bedankt voor deze heerlijke SOG-tijd!
(P.S. De wrijving berekeningen zijn iets moeilijker, dus die heb ik niet gespecificeerd.)

 is als volgt:
is als volgt: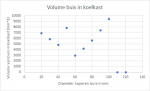

 ..
..
 ). Kost niets (alleen even een
). Kost niets (alleen even een 